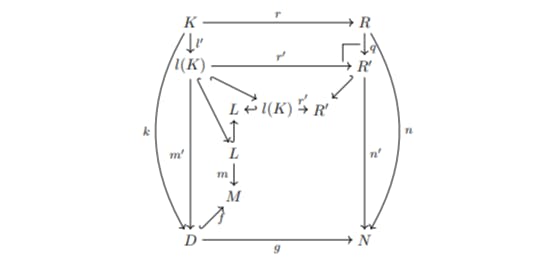
"The operation of deletion in graph transformations is complex in category theory, lacking a complement notion, which challenges existing frameworks and methods like the double pushout."
"Rule-based transformations involve substituting subgraphs using graph operations, with the addition of edges represented as a pushout while addressing the difficulty of deletion in categorical terms."
The article explores the complexities of graph transformations in category theory, particularly focusing on rule-based transformations that involve substituting subgraphs. Deletion operations pose significant challenges, as there is no categorical representation of complements, complicating the framework. The double pushout method is a prevalent solution, and the article discusses conditions that ensure the uniqueness of certain constructions while navigating the intricacies of morphisms, limits, and algebras within monographs, offering insight into ongoing research in Algebraic Graph Transformation.
Read at Hackernoon
Unable to calculate read time
Collection
[
|
...
]