Optimization by decoded quantum interferometry - Nature

"NP-hardness results indicate that finding exact optima and even sufficiently good approximate optima for worst-case instances of many optimization problems is probably out of reach for polynomial-time algorithms both classical and quantum4. Nevertheless, there remain combinatorial optimization problems, such as the closest vector problem, for which there is a large gap between the best approximation achieved by a polynomial-time classical algorithm5 and the strongest complexity-theoretic inapproximability result6."

"When considering average-case complexity, such gaps become more prevalent, as few average-case inapproximability results are known. These gaps present a potential opportunity for quantum computers, namely achieving in polynomial time an approximation that requires superpolynomial time to achieve using known classical algorithms. Quantum algorithms for combinatorial optimization have been the subject of intense research over the last three decades7,8,9,10,11,12,13, which has uncovered some evidence of a possible superpolynomial quantum speed-up for certain optimization problems14,15,16,17,18,19,20."

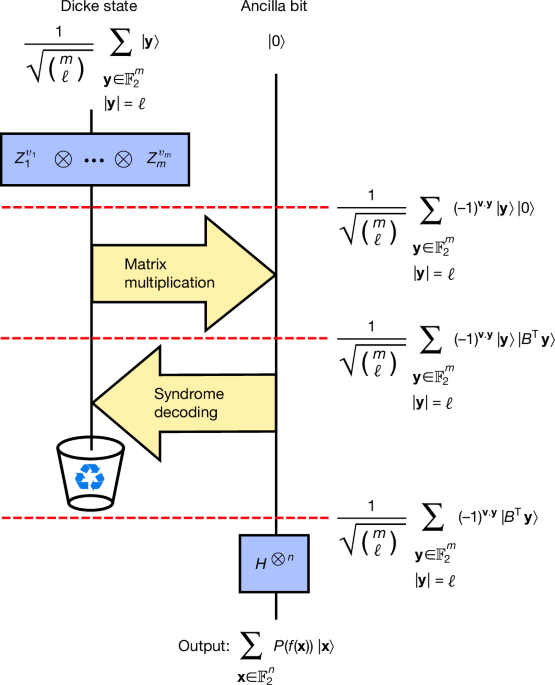
"We call this algorithm decoded quantum interferometry (DQI). DQI uses a quantum Fourier transform to arrange that amplitudes interfere constructively on symbol strings for which the objective value is large, thereby enhancing the probability of obtaining good solutions upon measurement. Most previous approaches to quantum optimization have been Hamiltonian-based7,8, with a notable exception being the superpolynomial speed-up due to Chen, Liu"

NP-hardness implies that computing exact optima or strong approximations for worst-case combinatorial optimization instances is infeasible for polynomial-time classical and quantum algorithms. Certain problems, like the closest vector problem, exhibit large gaps between best polynomial-time classical approximations and known inapproximability results. Average-case complexity often shows even larger gaps because few average-case inapproximability results exist. Those gaps create opportunities for quantum algorithms to produce polynomial-time approximations that are classically superpolynomially costly. Decoded Quantum Interferometry (DQI) leverages interference and the quantum Fourier transform to amplify amplitudes of high-objective-value symbol strings, increasing the chance of sampling good solutions. Many prior quantum optimization approaches used Hamiltonian-based methods, while some Fourier-based techniques serve as notable exceptions.

Read at Nature