New Knot Theory Discovery Overturns Long-Held Mathematical Assumption

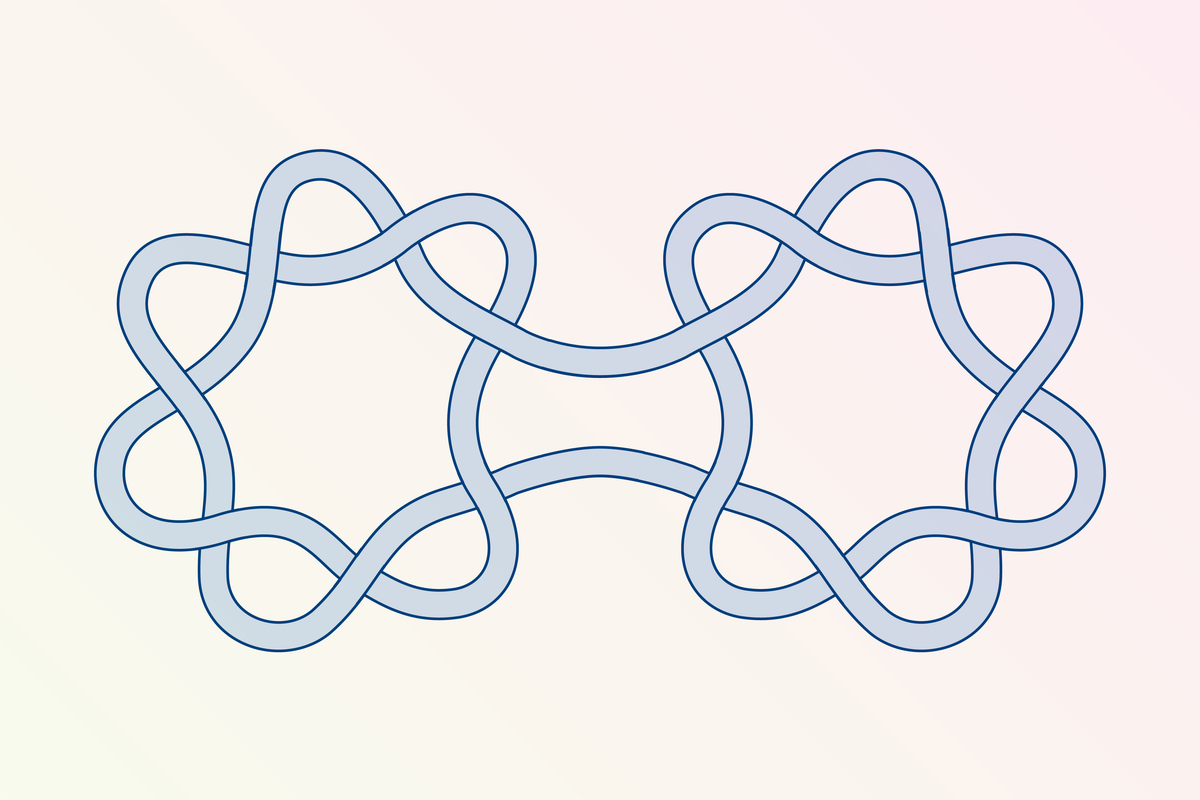
"Mathematicians long believed that if you attach cut ends of two different knots to each other, the new knot will be just as complex as the sum of the individual knots' complexity. But researchers recently managed to find a knot that is simpler than the sum of its parts. Knot theory is a branch of topology that has surprisingly practical applications, such as understanding how proteins coil DNA and how molecular structures remain stable."

"The theory's central question: How can we tell which knots are unique or which are the same as others? Mathematicians consider two knots the same if one can be manipulated to look like the other without being cut openany knots you can produce with mere tugging and pulling are fundamentally the same. Only cutting and reconnecting to let two strands cross yields unique knots. Using these careful manipulations, mathematicians assign each knot an unknotting number, which is the minimum number of cutting and reconnecting moves it would take to unravel the knot into a simple loop."

"Many mathematicians assumed that if we construct a larger knot by joining together smaller ones whose unknotting numbers are known, then the quickest way to untangle the larger knot will be by simply undoing each piece independently. This idea that two conjoined knots' unknotting numbers can be added was first proposed as a conjecture by Hilmar Wendt in a 1937 paper"

Knot theory classifies loops in three-dimensional space by allowing deformations without cutting; only cutting and reconnecting can create fundamentally new knots. Each knot receives an unknotting number equal to the minimum number of cut-and-reconnect moves required to turn it into a simple loop. Unknotting numbers are difficult to compute in many cases. For decades mathematicians believed unknotting numbers were additive under knot composition, a conjecture proposed by Hilmar Wendt in 1937. A concrete counterexample shows a composite knot whose unknotting number is lower than the sum of its components, disproving the long-standing additivity conjecture.

Read at www.scientificamerican.com