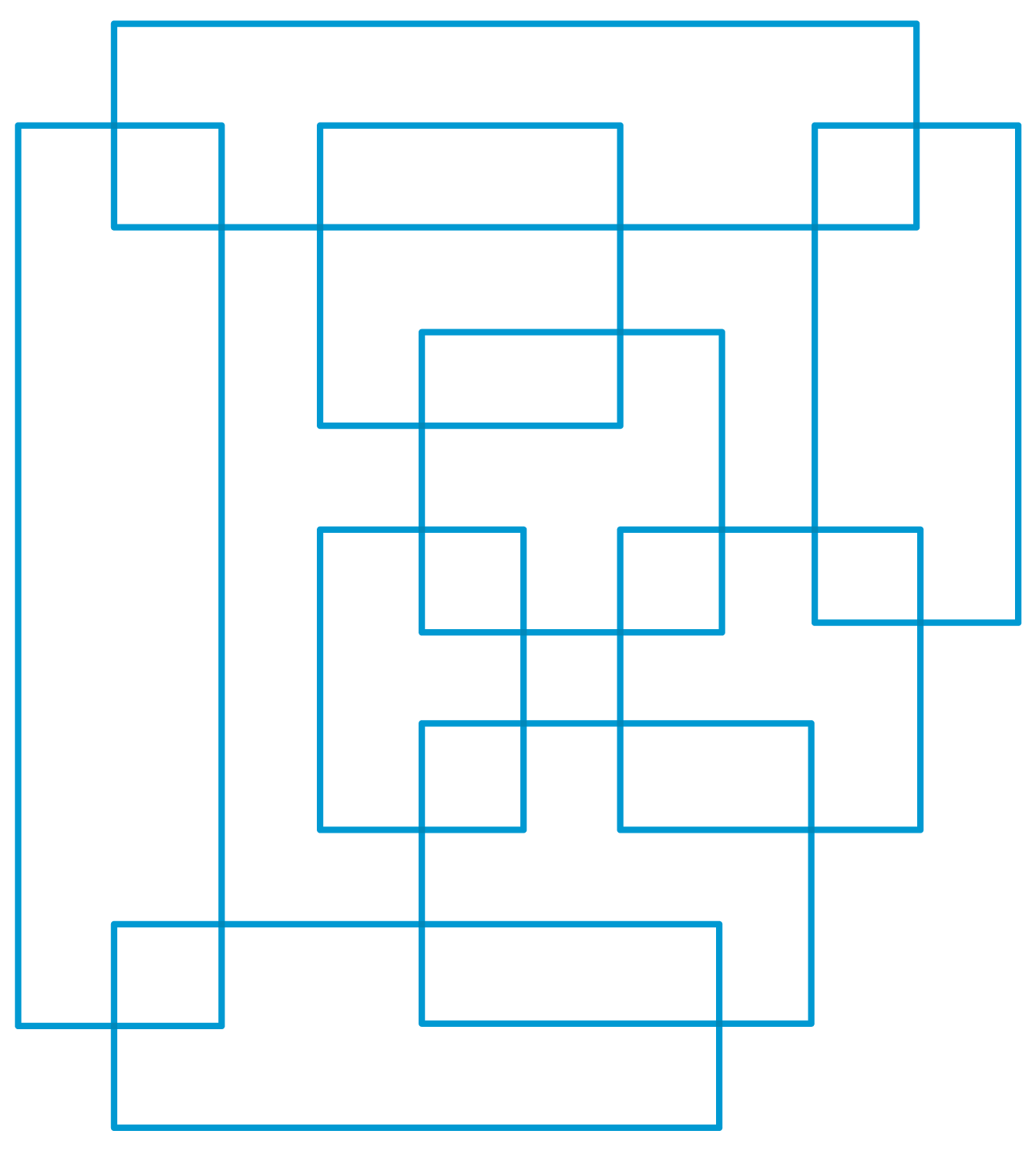
"The nine rectangles A, B, C, D, E, F, G, H and I overlap one another. Rectangle A intersects rectangles D and F; this relation can be written in shorthand as A\(D, F). Furthermore, B\(F, G) C\(G, H) D\(A, H) E\(H, I) F\(A, B, I) G\(B, C, I) H\(C, D, E) I\(E, F, G) Label the rectangles correctly with the letters A to I."
"Only the four blue-shaded rectangles below intersect three other rectangles, and therefore they must be F, G, H and I. H doesn't intersect F, G or I, whereas I intersects both F and G. Consequently, H is the topmost blue-shaded rectangle, and I is the third from the top. Because B\(F, G) and E\(H, I), the two rectangles B and E also can be identified. The rest is simple."
Nine rectangles labeled A–I overlap with specified pairwise intersections: A(D, F), B(F, G), C(G, H), D(A, H), E(H, I), F(A, B, I), G(B, C, I), H(C, D, E), I(E, F, G). Only four rectangles intersect three other rectangles; those are F, G, H, and I. H does not intersect F, G, or I, while I intersects both F and G, placing H topmost among the four blue-shaded rectangles and I third from the top. Knowing B(F, G) and E(H, I) identifies rectangles B and E, and the remaining labels follow by elimination.
Read at www.scientificamerican.com
Unable to calculate read time
Collection
[
|
...
]