"The chiral fermions in the topological states facilitates efficient spin and orbital angular momentum transport and play a crucial part in quantum electronics devices such as interferometers5,10,11,12,13,14. Meanwhile, chiral topological states in proximity with superconductors or magnets can lead to applications in quantum computing15 and cryogenic memories16. Thus, achieving mesoscopic coherent transport of chiral fermions in these topological states is crucial to realizing low-power topological electronics."
"However, access to these states in a typical topological metal is often limited because of the concurrent transport of electrons in trivial states20. The separation of the contributions of topological states from trivial states in their transport response is important21,22. Moreover, the linear electrical response of chiral fermions are innately zero because of the averaging of contributions from topological states with opposite Chern number under time-reversal symmetry (TRS)23."
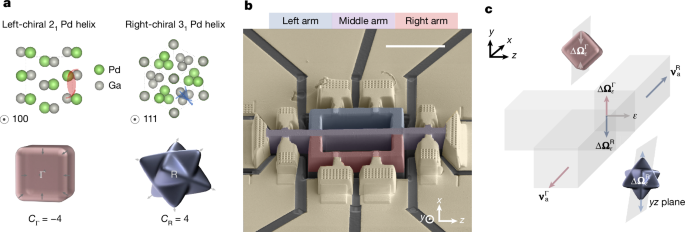
Chiral fermions in topological states enable efficient spin and orbital angular momentum transport and are integral to quantum electronic devices and superconducting or magnetic proximity applications. Mesoscopic coherent transport of these fermions is essential for low-power topological electronics. Typical topological metals suffer concurrent transport from trivial states, complicating access to topological-state transport. Linear electrical response of chiral fermions cancels under time-reversal symmetry due to opposite Chern numbers, so an occupancy imbalance between right- and left-chiral fermions is required in nonmagnetic materials to observe transport effects. Filtering trivial-state conduction while creating chirality imbalance allows study of chiral fermion transport without applying magnetic fields.
Read at Nature
Unable to calculate read time
Collection
[
|
...
]